About Mathematics and Real World Mathematics Applications
Unlocking the secrets of quantitative reasoning. Rewiring your existing math knowledge into a new, powerful web of innovation generating ideas. Axioms Discovery, Axiomatic Frontiers, Directional Thinking, Specific Consequences, Logic, Intuition, Innovation, Invention.
Saturday, June 11, 2022
The Best References in Set Theory
Saturday, March 26, 2022
Wednesday, March 23, 2022
For Aspiring Software Developers - how to link diagram with coding
Now, you will know! See this illustrations. Taken from one book about Java 3D programming.
This illustration shows relationships between coding and a diagram. You should also consider STACK manipulation approach too, because it boils down to stack push, pop, operation, operand, memory.
Thursday, March 17, 2022
How to Better Approach New Concepts in Math or in Any Field
You have, at your disposal, three mind faculties:
- Thought Initiator© - for thought inception and creation
- Thought Pusher© , or Referencer© - for manipulating thoughts
- Thought Visitor© - to visit established thoughts
With these faculties you manipulate thoughts in accordance to your wishes and motivations. Motivation is a mind state. Emotion is an idea. In order to effectively use these three faculties you consider everything as an idea or representations in brain, or mind. This includes complex structures like emotions, other ideas, objects, sensory inputs. Each of these have their representation in brain, mind and can be used to control them in order to take some actions or come up with new ideas.
Many talk about awareness. This is often understood as some kind of meditation state. But there is more to it. In order to take full advantage of 'meditation' the awareness needs to be connected with these three faculties. With Thought Visitor© you visit various thoughts and state of minds (which are considered as a thought object, and idea) and see where they come from, when did you create them, and how they can be manipulated in your advantage. For instance, language is based on references. But, you form references using Thought Initiator© and Thought Pusher©. These are powerful tools of your mind and brain. A proof or demonstration of existence of Thought Initiator© can be the event when you send command to your nose to smell. This is Thought Initiator© ordering mind circuitry to smell. In the same way you can visit an idea, decipher from which axioms (postulates!) is derived from and manipulate it with your initiatives. Similarly, you identify two or more objects or concepts and using Thought Initiator© you form references and manipulate references or associations between these objects or concepts
With these tools at hand we can discuss how to better approach new concepts in math. Usually, how we learn math is by reading. We form references to concepts from words outlined in the text. But these words are borrowed from everyday life and often confuse us as we try to match their meaning with the referenced mathematical concept.
Instead of going following path from term to concept as shown in the picture, you need to follow path of the blue line. This means mask (hide!) the word used as reference and form an object thought from the side of theorems, definitions, and postulates that created or led to the math concept of interest. The math concept you want to understand has to be, as close as possible, explained and defined using set concepts, because almost all math concept, no matter how misleading are the terms that reference them can be explained by using set theory.
Digression: problem with education is that student has more difficulty to associate a reference word to referenced concept instead of focusing on referenced concept, how it is derived, what are the major postulates and how it is instantiated from its axiomatic system it belongs to.
As for other fields, other than math, the approach is similar. The term may need to be masked or replaced with your own reference, while the surrounding system needs to be defined from theorems, definitions, and postulates. Also, what is theorem in one system can be axiom or starting postulate in another. This is how you can creatively and effectively link systems from different fields like between math and biochemistry or biology and mechanical engineering. This method I developed for multidisciplinary teams I call Postulate Driven Implicative Truth Synthesis. More on this in my book, "Yes, You Can!".
Sunday, March 13, 2022
The Role of Mind's Reference System in Our Understanding of Various Concepts
Felix Hausdorff used Old Greek words and letters for set theoretical concepts in his book, "Set Theory". But Greeks did not have set theory, so how Felix chose a word from Greek language for an nonexistent concept? Moreover, how a Greek or Latin word can be used for referring to a technology or mathematical concept, one that did not exist in that civilization, and is it a better way to do that rather than using a word from the language you know? It become evident how important is our inherent ability to create references, which are arbitrary in nature, but we want some kind of correlation with the meaning we know with the properties of a concept we are referring to. This, then, tells us that we can create truly arbitrary references, associations, relations, correlations, links between concepts, namely a reference name for an underlying concept.
If we can use a Greek or Latin word to refer to a concept (mathematical, engineering, or any other) that did not exist in their time and still can benefit from these references (we can manipulate them) then we can chose any word from any language to reference that concept. And this brings us to the point that we can conclude that the referenced concept is way more important than the reference word we are using to refer to it.
Our goal is to somehow manipulate concepts and their relationships as a whole using some kind of reference method, using references. Before that we need to understand as completely as we can the underlying inter-correlated concepts - concepts and their relationships, I will call it underlying system. What is the best way to do it? The answer is that they have to be understood in terms of the underlying axioms - we need to be aware of axioms and chosen postulates the underlying system is constructed from. In other words, we expect that underlying system needs to be axiomatized. We can give a best shot to axiomatize it and in many cases this can be a tough task, however, we need to have the best axioms we can come up with. Once the axioms are defined or discovered, postulates that define the underlying system components are discovered and identified we can move on to forming references to it. Then a more abstract step is required. We need to identify the fundamental concepts from which all the system elements are derived or constructed from. For instance, in math it is sets and operations on sets, in set theory it is a set membership relation (element x belongs to set A), in computer engineering is a structure stack and manipulation of it.
When acquiring new knowledge (in mathematics, engineering, or from most other fields) we often have to deal with reference words (references) put out by the authors of the book we are reading. In order to effectively acquire new knowledge, these references need to be masked! We have to cover them with a "cloth" so we can uncover the underlying system, with its axioms and postulates, referenced with now masked word. Then, we replace the masked word with a reference word of our choice. Why the masking is necessary? Because we are inclined to seek the link between the meaning of the reference word we already know, from its everyday use, and somehow use that to describe underlying mathematical, engineering (or other scientific) concept. This in many cases leads to confusion. The reference word can be misguided and misleading to us in our effort to understand the underlying referenced concept. It is misleading because we try to match the everyday meaning of the word with concepts, or their properties, within axiomatized system which is very specific and in many cases disconnected from ordinary word usage. That's why it is more beneficial to use an Old Greek or Latin word for a reference rather than a non-productive metaphor from ordinary word usage. As a matter of fact you can refer to any mathematical concept with randomly chosen strings of letters, like "aadvark12" to describe any mathematical concept, because this reference will not misguide you to seek match between its ordinary use (which it does not exist in this case) and underlying mathematical concept (which, anyway, can be described with set theoretical terms, which in turn can be reduced to the statements 'x belongs to set A', i.e. membership relations.) If the word 'aadvark12' does not exist in a dictionary that does not reduce in any way our understanding of the underlying concept; moreover it prevents us to use everyday word to refer to it and then be misguided. On the other hand, if a word is in the dictionary, it does not mean it is an effective reference to a mathematical concept.
More on this and how to link different axiomatized systems from different fields using Implicative Truth Synthesis and how to recognize and utilize Thought Initiator©, Thought Pusher©, Thought Visitor© mind faculties, in my book, "Yes, You Can!".
Saturday, March 12, 2022
Monday, February 21, 2022
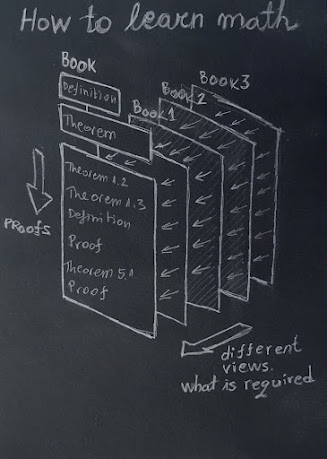
How to learn math
How to learn math. Reviewing several books with same topic opens different views on the same subject. Within a book you use definitions and previously proved theorems to prove new theorems. Postulating sets is essential. #education #math #engineering